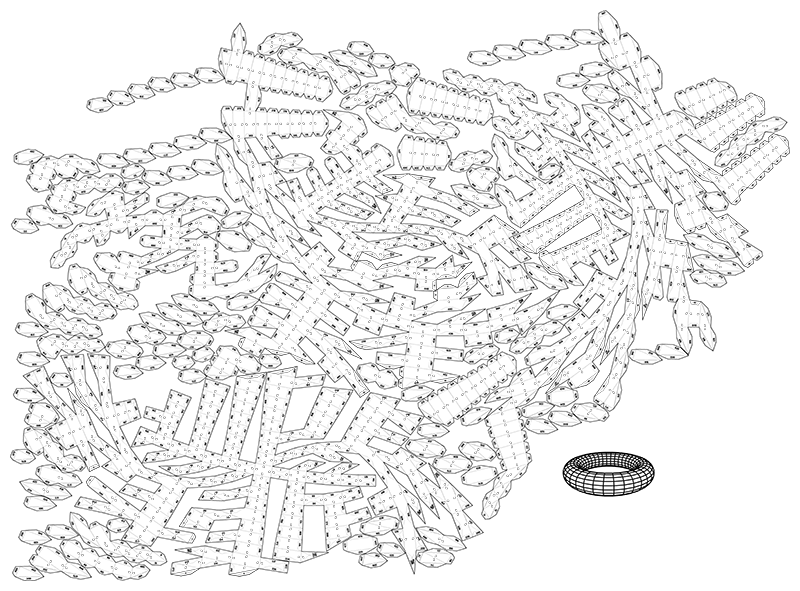
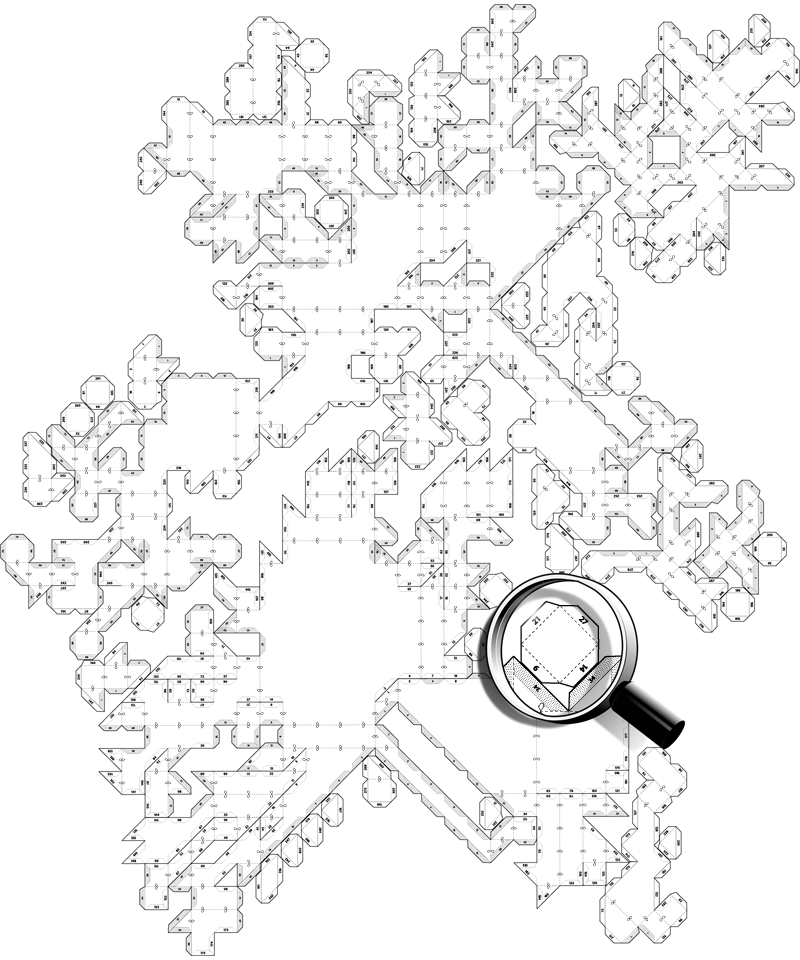
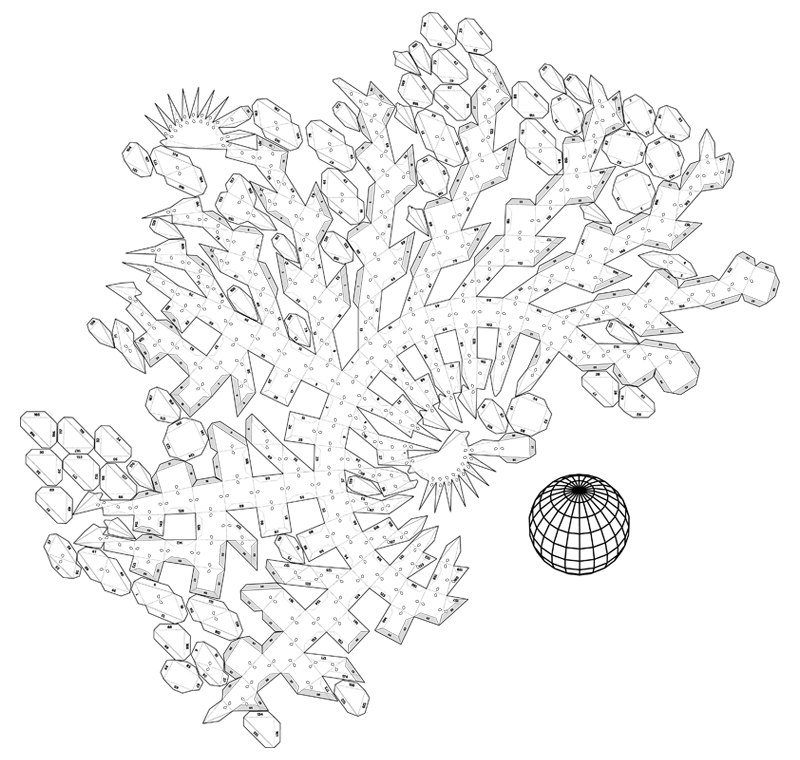
Papercraft, Unfolding 3D
A three-dimensional computer model is translated into a two-dimensional representation: a flat surface. This process is also known as UV mapping.
General
I wondered how all the pieces could be put together in a minimum amount of space.
The number of possibilities is huge, and they cannot all be calculated.
If you are interested in converting your 3D object into a 2D projection, please feel free to send me an email at arjan@drububu.com
Some papercraft models buckyball cube tetrahedron octahedron dodecahedron icosahedron spiked-dodacahedron sphere torus and drububu .
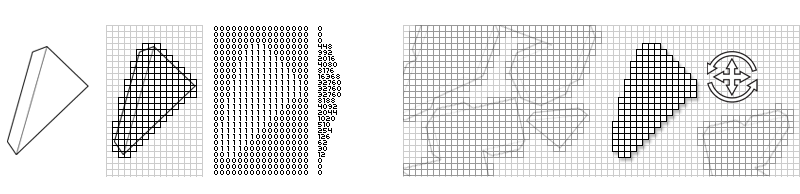
The retro game Tetris
gave me a clue as to how to solve this problem.
By using slightly more complex Tetris objects, it is possible to
position the individual pieces in a limited amount of space without
having them intersect each other.
Each piece is transformed into a series of squares.
![]() There are only 10 types of people in the world,
those who understand binary, and those who don't
There are only 10 types of people in the world,
those who understand binary, and those who don't
![]()
A computer uses bytes and bits. A bit may represent either zero or one. A byte is a series of bits.
A byte consists of 8 bits. The first bit in a byte represents number 1,
the second number 2, the third number 4 etc.
A byte - 8 bits - can store numbers from 0 to 255.
E.g. the decimal number - numbers used by people - 59 is represented by the binary number - numbers used internally by computer - 00111011 (read from the right to the left).
Depending on your computer system, a number is represented by either 4 or 8 bytes.
Suppose your system uses 4 bytes, or 32 bits to represent a number.
Each bit is used for an individual square. If a square contains part of
the piece a bit is switched on, if not, the bit is switched off.
One single number can store the information of 32 squares, and depending on the presence of squares, a bit in the number can be either switched on or off. The exact number depends on the question as to which bits are switched on or off.
A series of numbers represents an individual piece.
If a piece is large, you'll need relatively more numbers, if a piece is
small, less numbers will do.
OK, that's a lot of theory, why all this fuzz?
The available area is divided into squares that have the same size as the squares that form a piece.
Each square within the available area may be covered by just one piece.
Just like the individual pieces, the available area is represented by a series of numbers. Each number is used to store the information of 32 squares.
If a bit is switched on, it means that the square is occupied, if a bit is switched off, the square is available.
To check if a piece can be put at a certain position in the available area, we need to check if all the squares which represent the piece are available in the area.
The computer, by using the so-called logical AND operator, is able to calculate very quickly whether pieces will intersect at a specific position.
Logical AND compares two numbers and checks which mutual bits are switched on.
If two bits at the same position in a byte or number are switched on, the result of a logical AND operation is a number with a bit switched on at that specific position.
All other combinations of bits switched on or off at a certain position, are switched off as a result of a Logical AND operation.
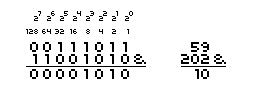
The result of a logical AND is a new number, in the example 10.
The exact number calculated by the Logical AND operation is not very important.
If the result is not equal to zero, both numbers share at least one bit, which is switched on. In this case, two pieces intersect, which is wrong, since pieces should not intersect.
If the result is zero, none of the numbers share one or more bits which are switched on at a certain position, which is OK since the pieces should not intersect.
A piece is represented by a series of numbers, so all the numbers need to be checked to make sure that the complete piece does not intersect with any pieces that have already been positioned in the available area.
The computer, by using the logical AND operation, is able to calculate at once if any of the 32 squares will intersect.
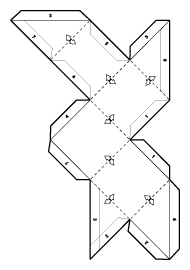
To make sure that a minimum amount of space is used, all the pieces are
checked at every position in the available area.
The pieces are also rotated, like in Tetris, so it is possible to find
an optimal minimum within a reasonable amount of time.
The above described process is repeated several times, and each time the pieces are positioned in a different order.
Technically speaking, the best option is the option that requires the
smallest surface.
Artistically speaking, the best option is not always the option that
requires the smallest surface.